3.1. Design documentation¶

3.1.1. Overview¶

The Antenna module provides:

a class (Angles) and utility functions to deal with angles

a base class (AntennaModel) that provides an interface for the modeling of the radiation pattern of an antenna;

a set of classes derived from this base class that each models the radiation pattern of different types of antennas;

a base class (PhasedArrayModel) that provides a flexible interface for modeling a number of Phase Antenna Array (PAA) models

a class (UniformPlanarArray) derived from this base class, implementing a Uniform Planar Array (UPA) supporting both rectangular and linear lattices

3.1.2. Angles¶

The Angles class holds information about an angle in 3D space using spherical coordinates in radian units. Specifically, it uses the azimuth-inclination convention, where

Inclination is the angle between the zenith direction (positive z-axis) and the desired direction. It is included in the range [0, pi] radians.
Azimuth is the signed angle measured from the positive x-axis, where a positive direction goes towards the positive y-axis. It is included in the range [-pi, pi) radians.

Multiple constructors are present, supporting the most common ways to encode information on a direction. A static boolean variable allows the user to decide whether angles should be printed in radian or degree units.

A number of angle-related utilities are offered, such as radians/degree conversions, for both scalars and vectors, and angle wrapping.

3.1.3. AntennaModel¶

The AntennaModel uses the coordinate system adopted in [Balanis] and depicted in Figure Coordinate system of the AntennaModel. 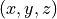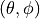This system is obtained by translating the Cartesian coordinate system used by the ns-3 MobilityModel into the new origin $o$ which is the location of the antenna, and then transforming the coordinates of every generic point $p$ of the space from Cartesian coordinates $(x,y,z)$ into spherical coordinates $(r, \theta,\phi)$ . The antenna model neglects the radial component $r$ , and only considers the angle components $(\theta, \phi)$ . An antenna radiation pattern is then expressed as a mathematical function $g(\theta, \phi) \longrightarrow \mathcal{R}$ that returns the gain (in dB) for each possible direction of transmission/reception. All angles are expressed in radians.

Coordinate system of the AntennaModel¶

3.1.4. Single antenna models¶

In this section we describe the antenna radiation pattern models that are included within the antenna module.

3.1.4.1. IsotropicAntennaModel¶

This antenna radiation pattern model provides a unitary gain (0 dB) for all direction.

3.1.4.2. CosineAntennaModel¶

This is the cosine model described in [Chunjian]: the antenna gain is determined as:

$g(\phi, \theta) = \cos^{n} \left(\frac{\phi - \phi_{0}}{2} \right)$

where $\phi_{0}$ is the azimuthal orientation of the antenna (i.e., its direction of maximum gain) and the exponential

$n = -\frac{3}{20 \log_{10} \left( \cos \frac{\phi_{3dB}}{4} \right)}$

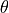determines the desired 3dB beamwidth $\phi_{3dB}$ . Note that this radiation pattern is independent of the inclination angle $\theta$ .

A major difference between the model of [Chunjian] and the one implemented in the class CosineAntennaModel is that only the element factor (i.e., what described by the above formulas) is considered. In fact, [Chunjian] also considered an additional antenna array factor. The reason why the latter is excluded is that we expect that the average user would desire to specify a given beamwidth exactly, without adding an array factor at a latter stage which would in practice alter the effective beamwidth of the resulting radiation pattern.

3.1.4.3. ParabolicAntennaModel¶

This model is based on the parabolic approximation of the main lobe radiation pattern. It is often used in the context of cellular system to model the radiation pattern of a cell sector, see for instance [R4-092042a] and [Calcev]. The antenna gain in dB is determined as:

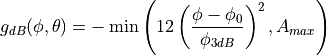
$g_{dB}(\phi, \theta) = -\min \left( 12 \left(\frac{\phi - \phi_{0}}{\phi_{3dB}} \right)^2, A_{max} \right)$

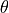where $\phi_{0}$ is the azimuthal orientation of the antenna (i.e., its direction of maximum gain), $\phi_{3dB}$ is its 3 dB beamwidth, and $A_{max}$ is the maximum attenuation in dB of the antenna. Note that this radiation pattern is independent of the inclination angle $\theta$ .

3.1.4.4. ThreeGppAntennaModel¶

This model implements the antenna element described in 38901. Parameters are fixed from the technical report, thus no attributes nor setters are provided. The model is largely based on the ParabolicAntennaModel.

3.1.5. Phased Array Model¶

The class PhasedArrayModel has been created with flexibility in mind. It abstracts the basic idea of a Phased Antenna Array (PAA) by removing any constraint on the position of each element, and instead generalizes the concept of steering and beamforming vectors, solely based on the generalized location of the antenna elements. For details on Phased Array Antennas see for instance [Mailloux].

Derived classes must implement the following functions:

GetNumElems: returns the number of antenna elements
GetElementLocation: returns the location of the antenna element with the specified index, normalized with respect to the wavelength
GetElementFieldPattern: returns the horizontal and vertical components of the antenna element field pattern at the specified direction. Same polarization (configurable) for all antenna elements of the array is considered.

The class PhasedArrayModel also assumes that all antenna elements are equal, a typical key assumption which allows to model the PAA field pattern as the sum of the array factor, given by the geometry of the location of the antenna elements, and the element field pattern. Any class derived from AntennaModel is a valid antenna element for the PhasedArrayModel, allowing for a great flexibility of the framework.

3.1.5.1. UniformPlanarArray¶

The class UniformPlanarArray is a generic implementation of Uniform Planar Arrays (UPAs), supporting rectangular and linear regular lattices. It closely follows the implementation described in the 3GPP TR 38.901 38901, considering only a single panel, i.e., $N_{g} = M_{g} = 1$ .

By default, the antenna array is orthogonal to the x-axis, pointing towards the positive direction, but the orientation can be changed through the attributes “BearingAngle”, which adjusts the azimuth angle, and “DowntiltAngle”, which adjusts the elevation angle. The slant angle is instead fixed and assumed to be 0.

The number of antenna elements in the vertical and horizontal directions can be configured through the attributes “NumRows” and “NumColumns”, while the spacing between the horizontal and vertical elements can be configured through the attributes “AntennaHorizontalSpacing” and “AntennaVerticalSpacing”.

UniformPlannarArray supports the concept of antenna ports following the sub-array partition model for TXRU virtualization, as described in Section 5.2.2 of 3GPP TR 36.897 [3GPP_TR36897]. The number of antenna ports in vertical and horizontal directions can be configured through the attributes “NumVerticalPorts” and “NumHorizontalPorts”, respectively. For example, if “NumRows” and “NumColumns” are configured to 2 and 4, and the number of “NumVerticalPorts” and “NumHorizontalPorts” to 1 and 2, then the antenna elements belonging to the first two columns of the antenna array will belong to the first antenna port, and the third and the fourth columns will belong to the second antenna port. Note that “NumRows” and “NumColumns” must be a multiple of “NumVerticalPorts” and “NumHorizontalPorts”, respectively.

Whether the antenna is dual-polarized or not is configured through the attribute “IsDualPolarized”. In case the antenna array is dual polarized, the total number of antenna elements is doubled and the two polarizations are overlapped in space. The polarization slant angle of the antenna elements belonging to the first polarization are configured through the attribute “PolSlantAngle”; while the antenna elements of the second polarization have the polarization slant angle minus 90 degrees, as described in 38901 (i.e., ${\zeta}$ ).

3.1.5.2. CircularApertureAntennaModel¶

The class CircularApertureAntennaModel implements the radiation pattern described in 38811. Specifically, the latter represents parabolic antennas, i.e., antennas which are typically used for achieving long range communications such as earth-to-satellite links. The default boresight orientation is parallel to the positive z-axis, and it can be tuned by using the AntennaInclination and AntennaAzimuth parameters. This implementation provides an exact characterization of the antenna field pattern, by leveraging the standard library Bessel functions implementation introduced with C++17. 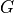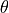Accordingly, the antenna gain $G$ at an angle $\theta$ from the boresight main beam is evaluated as:

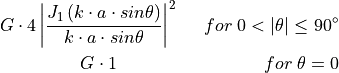
$G \cdot 4\left | \frac{J_{1}\left ( k\cdot a\cdot sin\theta \right )}{k\cdot a\cdot sin\theta} \right |^{2}\;\;\;\;\; for\; 0<\left | \theta \right |\leq 90^{\circ} \\ G \cdot 1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; for\; \theta=0$

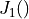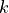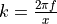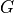where $J_{1}()$ is the Bessel function of the first kind and first order, and $a$ is the radius of the antenna’s circular aperture. The parameter $k$ is equal to $k=\frac{2\pi f}{x}$ , where $f$ is the carrier frequency, and $c$ is the speed of light in vacuum. The parameters $G$ (in logarithmic scale), $a$ and $f$ can be configured by using the attributes “AntennaMaxGainDb”, “AntennaCircularApertureRadius” and “OperatingFrequency”, respectively. This type of antennas features a symmetric radiation pattern, meaning that a single angle, measured from the boresight direction, is sufficient to characterize the radiation strength along a given direction.

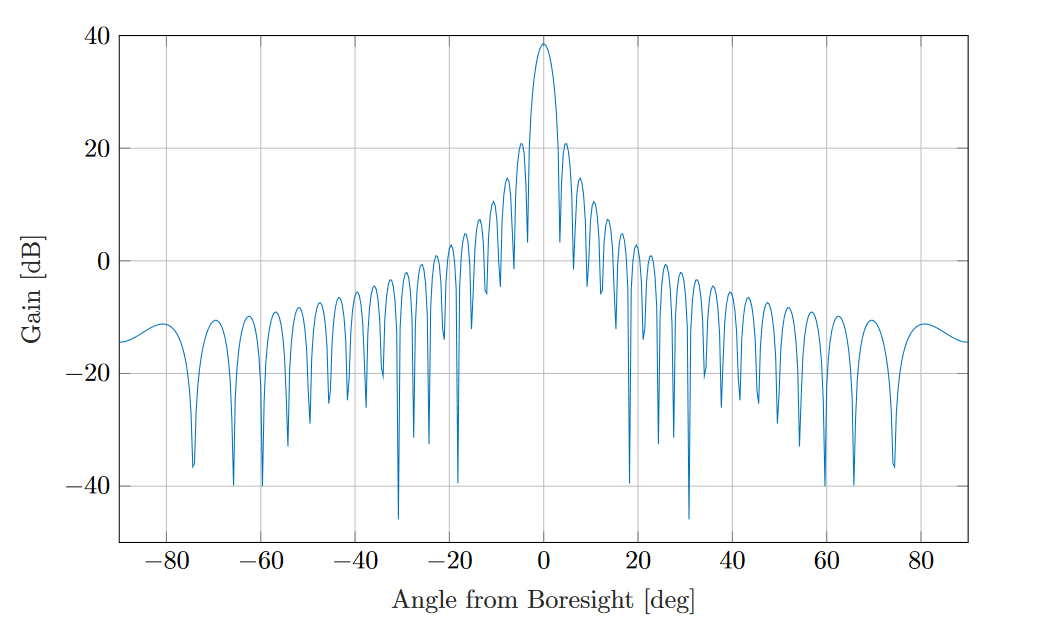
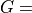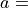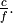
Circular aperture antenna radiation pattern with $G =$ 38.5 dB and $a =$ 10 $\frac{c}{f}.$ ¶

Balanis: C.A. Balanis, “Antenna Theory - Analysis and Design”, Wiley, 2nd Ed.
Chunjian(1,2,3): Li Chunjian, “Efficient Antenna Patterns for Three-Sector WCDMA Systems”, Master of Science Thesis, Chalmers University of Technology, Göteborg, Sweden, 2003
Calcev: George Calcev and Matt Dillon, “Antenna Tilt Control in CDMA Networks”, in Proc. of the 2nd Annual International Wireless Internet Conference (WICON), 2006
R4-092042a: 3GPP TSG RAN WG4 (Radio) Meeting #51, R4-092042, Simulation assumptions and parameters for FDD HeNB RF requirements.

38901(1,2,3): 3GPP. 2018. TR 38.901, Study on channel model for frequencies from 0.5 to 100 GHz, V15.0.0. (2018-06).
38811: 3GPP. 2018. TR 38.811, Study on New Radio (NR) to support non-terrestrial networks, V15.4.0. (2020-09).

Mailloux: Robert J. Mailloux, “Phased Array Antenna Handbook”, Artech House, 2nd Ed.
3GPP_TR36897: 3GPP. 2015. TR 36.897. Study on elevation beamforming / Full-Dimension (FD) Multiple Input Multiple Output (MIMO) for LTE. V13.0.0. (2015-06)